激光器谐振模

This is Section 6.1 of the Laser Optics Resource Guide.

激光束的形状由激光在增益介质中被放大所在的谐振腔决定。激光谐振器通常通过使用高反射率介质镜或利用全反射防止光逸散的单片晶体形成（图 1）。下面是常见的激光谐振腔几何结构列表¹:

平面平行谐振腔：两个平面反射镜之间的距离等于半个激光波长的整数倍
同心谐振腔：两个曲率半径相同、曲率中心重合的球面镜
共焦谐振腔：两个曲率半径相同、焦点重合的球面镜
环形谐振腔：由两个以上的反射镜组成的环形，其中，反射光的总闭环路径等于半个激光波长的整数倍

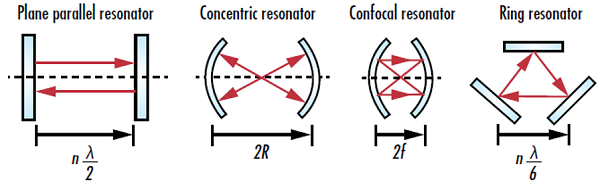
图 1: 四种常见类型的激光谐振腔的几何形状，其中，n 是整数值，λ 是激射波长，R 是曲面镜曲率半径，f 是曲面镜的焦距

如果反射光停留在腔内，即使反射次数接近无穷，谐振腔依然“稳定” (图 2)。在这种情况下，光只能通过部分反射镜离开谐振腔。另一方面，如果反射光随着反射次数趋于无穷而不断发散，谐振腔将被视为“非稳腔”。如果出现这种情况，光束的尺寸会一直增长，直到比反射镜更大，然后逸出系统。稳定谐振腔通常与功率高达2kW 的激光器一起使用，以实现高增益并改善方向性。非稳谐振腔通常使用于高功率激光器，以降低反射镜受损的几率。¹

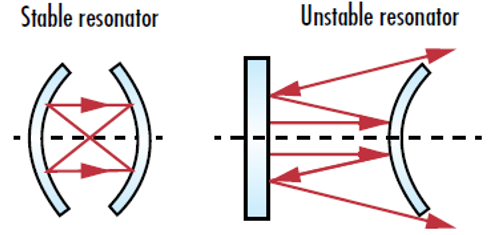
图 2: 稳定激光谐振器将所有反射光都保持在腔内，不稳定的谐振器则会导致反射光扩散，直到最终从腔内逸出

谐振腔的路径长度决定了纵向谐振腔模，或导致谐振腔内驻波的电场分布。光束的模态决定了它的形状。这些模态保留它们的振幅分布，并在完成谐振腔内的闭环路径后重现该分布（除了可能由于腔内的损耗而降低一些功率外）。为了实现谐振模，它还必须经历等于闭环路径 2π 的整数倍的相移（图 3）。

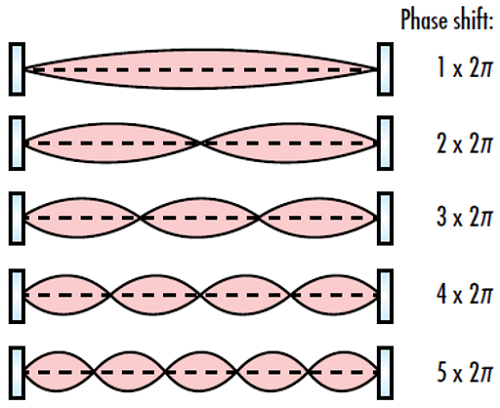
图 3: 光学谐振器内整个环路的相移必须是 2π 的整数倍，以便实现谐振模

最简单的激光谐振模是厄米高斯模，也称为横向电磁模(TEM_nm)，其中，电场分布可以近似为高斯函数与埃尔米特多项式的乘积 ²:

$$ E_{nm} \! \left(x, y, z \right) = E_0 \frac{w_0}{w \! \left( z \right)} \, \cdot \, H_{n} \left( \sqrt{2} \frac{x}{w \! \left( z \right)} \right) \cdot \exp{\left( -\frac{x^2}{w \! \left( z \right) ^2} \right)} \, \cdot \, H_m \left( \sqrt{2} \frac{y}{w \! \left( z \right)} \right) \cdot \exp{\left( -\frac{y^2}{w \! \left( z \right) ^2} \right)} \, \cdot \, \exp{\Bigg[ -i \left[ kz - \left( 1 + n + m \right) \cdot \tan^{-1}{\left( \frac{z}{z_R} \right)} + \frac{k \left( x^2 + y^2 \right)}{2 R \! \left( z \right) } \right] \Bigg]} $$

\begin{align} E_{nm} \! \left(x, y, z \right) = & \, E_0 \frac{w_0}{w \! \left( z \right)} \, \cdot \, H_{n} \left( \sqrt{2} \frac{x}{w \! \left( z \right)} \right) \\ & \cdot \exp{\left( -\frac{x^2}{w \! \left( z \right) ^2} \right)} \, \cdot \, H_m \left( \sqrt{2} \frac{y}{w \! \left( z \right)} \right) \cdot \exp{\left( -\frac{y^2}{w \! \left( z \right) ^2} \right)} \\ & \cdot \, \exp{\Bigg[ -i \left[ kz - \left( 1 + n + m \right) \cdot \tan^{-1}{\left( \frac{z}{z_R} \right)} + \frac{k \left( x^2 + y^2 \right)}{2 R \! \left( z \right) } \right] \Bigg]} \end{align}

或

$$ E_{nm} \! \left(x, y, z \right) = E_0 \cdot H_n \cdot H_m \frac{w_0 \, x \, y}{\left[ w \! \left( z \right) \right]^3} \cdot \exp{\left[ - \left( \frac{x}{w \! \left( z \right)} \right)^2 \right]} \cdot \exp{\left[ - \left( \frac{y}{w \! \left( z \right)} \right)^2 \right]} \cdot \exp{\Bigg[ -i \left[ kz - \left( 1 + n + m \right) \cdot \tan^{-1}{\left( \frac{z}{z_R} \right)} + \frac{k \left( x^2 + y^2 \right) }{2 R \! \left( z \right)} \right] \Bigg]} $$

\begin{align} E_{nm} \! \left(x, y, z \right) = & \, E_0 \cdot H_n \cdot H_m \frac{w_0 \, x \, y}{\left[ w \! \left( z \right) \right]^3} \cdot \exp{\left[ - \left( \frac{x}{w \! \left( z \right)} \right)^2 \right]} \cdot \exp{\left[ - \left( \frac{y}{w \! \left( z \right)} \right)^2 \right]} \\ & \cdot \exp{\Bigg[ -i \left[ kz - \left( 1 + n + m \right) \cdot \tan^{-1}{\left( \frac{z}{z_R} \right)} + \frac{k \left( x^2 + y^2 \right) }{2 R \! \left( z \right)} \right] \Bigg]} \end{align}

E₀ 是视场最大值
x 和 y 是定义光束横截面的轴
z 是传播轴
w₀ 是束腰
w(z) 是给定 z 值下的光束半径
H_n(x) 和 H_m(x) 是具有非负整数项 n 和 m 的埃尔米特多项式
k 是波数 (k=2π/λ)
z_R 是瑞利长度
R(z) 是波前的曲率半径

The integers n and m define the beam shape in the x and y directions, respectively. An ideal Gaussian beam is defined by the mode TEM₀₀, which occurs when n and m are both equal to 0 (Figure 4). For more information on Gaussian beams, please refer to our Gaussian Beam Propagation application note. All other values of n and m produce more complicated resonator modes.³ In Figure 5, the cross-sectional geometries of the lowest order Hermite-Gaussian modes with n and m values ranging from 0 to 3 are shown.

图 4: 厄米高斯谐振腔模 TEM₀₀ 对应于完美的高斯光束

图 5: n 和 m 值在 0 到 3 之间的最低阶厄米高斯分布谐振腔模的横截面

图 5: 6.5：n 和 m 值在 0 到 3 之间的最低阶厄米高斯分布谐振腔模的横截面

参考文献

“Section 2.6: Various Laser Resonators.” Advanced Manufacturing Laboratory, Columbia Engineering, www.aml.engineering.columbia.edu/ntm/level2/ch02/html/l2c02s06.html.
Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
Paschotta Rüdiger. Field Guide to Lasers. SPIE Press, 2008.

上个章节下个章节

本内容对您是否有用？

感谢您为本内容评分！