了解球透镜

球透镜是一种非常有用的光学元件，用于提高光纤、发射器及检测器之间的信号耦合。此外，它也适用于内镜、条码扫描、非球面透镜的预加工材料和传感器等应用。球透镜采用单一玻璃基片制造而成，可以聚焦或输出平行光，取决于输入源的几何形状。半球透镜也很常见，在应用的物理约束要求更紧凑型的设计的情况下，与（全）球透镜交换使用。

使用球透镜的基本方程式

共有五种需要了解和使用球透镜的主要参数（图1）：输入源的直径 $ \small{\left( d \right)} $、球透镜的直径 $ \small{\left( D \right)} $、球透镜的有效焦距 $ \small{\left( \text{EFL} \right)} $、球透镜的后焦距 $ \small{\left( \text{BFL} \right)} $ 和球透镜的折射率 $ \small{\left( n \right)} $。

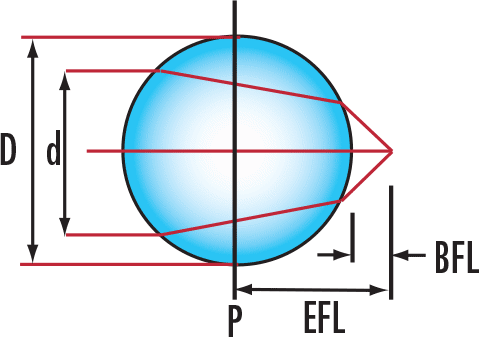
图 1： 主要参数

$ \small{\text{EFL}} $ 的计算方法非常简单（方程式1），这是因为它只有两种变量：球透镜的直径 $ \small{\left( D \right)} $ 和折射率 $ \small{\left( n \right)} $。$ \small{\text{EFL}} $是从球透镜的中心开始测量的，在图1中标示为R。一旦计算出EFL和$ \small{D} $后，即可轻易地计算出$ \small{\text{BFL}} $（方程式2）。数值孔径$ \small{\text{NA}} $（方程式3）则取决于$ \small{\text{EFL}} $和$ \small{d} $。它通常被引用及经常用来代替$ \tfrac{d}{D} $。

由于经常使用$ \small{\text{NA}} $，因此图2说明了随着输入光源直径 $ \small{\left( d \right)} $的提高$ \small{\text{NA}} $值将增大。

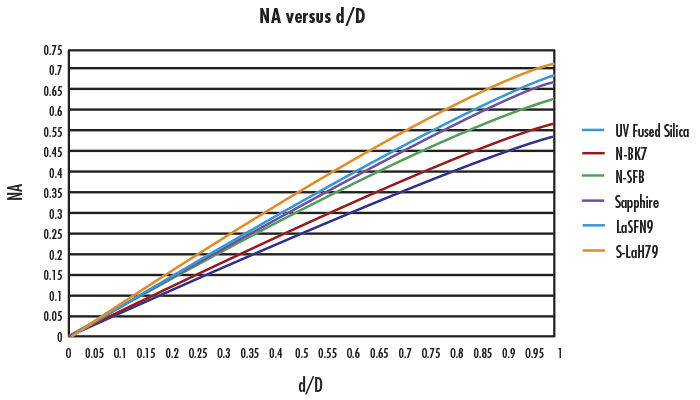
图 2： 爱特蒙特光学®提供的球透镜玻璃类型的数值孔径与直径的对比。

应用范例

范例 1：激光到光纤的耦合

将激光的光耦合到光纤时，球透镜的选择将取决于光纤的 $ \small{\text{NA}} $和激光光束的直径或输入源。激光光束的直径用来确定球透镜的 $ \small{\text{NA}} $。球透镜的 $ \small{\text{NA}} $必须低于或与光纤的 $ \small{\text{NA}} $相同，以耦合所有的光。光纤与球透镜间的接触所图 3 所示。

图 3： 激光到光纤的耦合

初始参数
输入激光光束的直径 = 2mm
球透镜的折射率 = 1.517
光纤的数值孔径 = 0.22

计算参数
球透镜的直径

>

6-8 毫米的 N-BK7 球透镜直径（折射率为 1.517）非常适合将 2 毫米的激光源耦合到 $ \small{0.22 \text{ NA}} $ 的光纤。可以轻易尝试不同的折射率以查找激光到光纤耦合应用的最佳球透镜。

范例 2：光纤到光纤的耦合

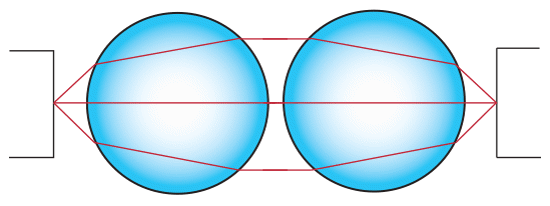
为了将其中一个光纤的光耦合到另一个具有相同 $ \small{\text{NA}} $ 的光纤，必须使用两个相同的球透镜。将两个球透镜与光纤放在一起，如图 4 所示。如果光纤具有相同的 $ \small{\text{NA}} $ ，则可应用如范例 1 所示的相同逻辑。

图 4： 光纤到光纤的耦合